
In geometry, right triangles are our friends, too. So together we will determine whether two triangles are congruent and begin to write two-column proofs using the ever famous CPCTC: Corresponding Parts of Congruent Triangles are Congruent. These include SSS, ASA, SAS, AAS postulates, where S stands for side and A stands for angle. Knowing these four postulates, as Wyzant nicely states, and being able to apply them in the correct situations will help us tremendously throughout our study of geometry, especially with writing proofs. 11) ASA S U T D SUT DUT 12) SAS W X V K VW XK 13) SAS B A C K J L CA LJ 14) ASA D E F J K L DE JK 15) SAS H I J R S T IJ ST 16) ASA M L K S T U L T 17) SSS R S Q D RS DQ 18) SAS W U V M K VW VM-2-Create your own worksheets like this one with Infinite Geometry. ASA and AAS are important when solving proofs. Another shortcut is angle-angle-side (AAS), where two pairs of angles and the non-included side are known to be congruent.
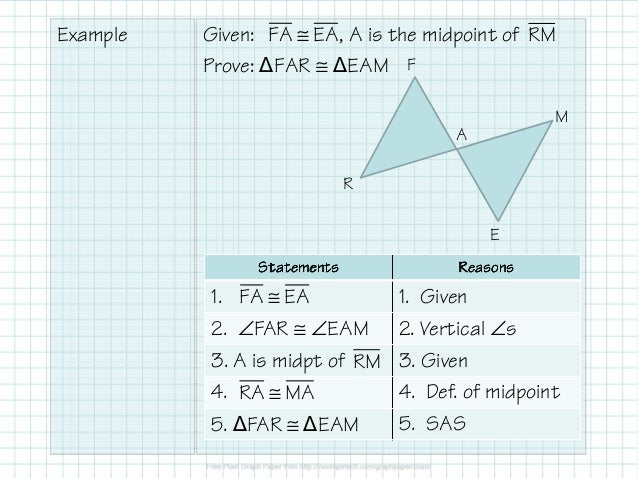
This shortcut is known as angle-side-angle (ASA). You must have at least one corresponding side, and you can’t spell anything offensive! If two pairs of corresponding angles and the side between them are known to be congruent, the triangles are congruent.
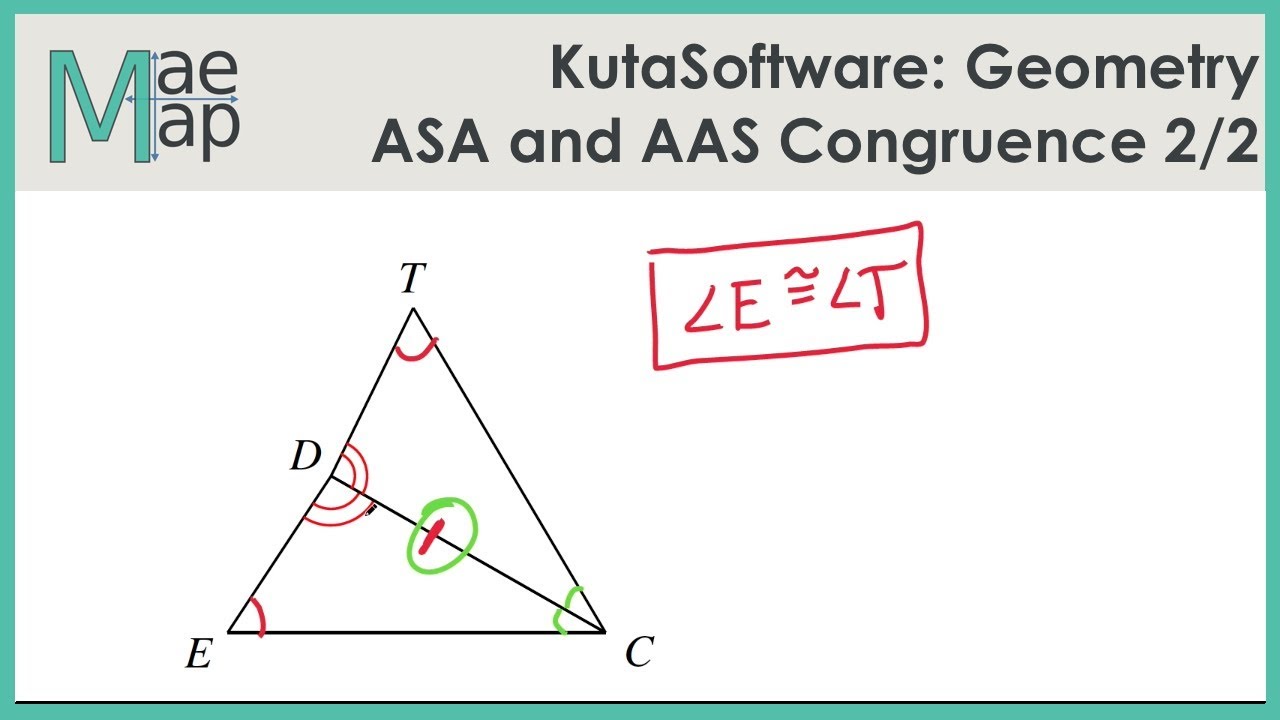
We will explore both of these ideas within the video below, but it’s helpful to point out the common theme. Likewise, SSA, which spells a “bad word,” is also not an acceptable congruency postulate. Every single congruency postulate has at least one side length known!Īnd this means that AAA is not a congruency postulate for triangles.

As you will quickly see, these postulates are easy enough to identify and use, and most importantly there is a pattern to all of our congruency postulates.


 0 kommentar(er)
0 kommentar(er)
